如何计算高频页面

这是个技术面试中常见的问题。给定一个长度为 \( n \) 的数组 \( A \) ，保证其中必定有多数派，多数派就是出现次数超过 \( \frac{n}{2} \) 的元素，你的任务就是找到多数派元素。元素类型可以是数字、URL、商品编号等。

这个问题可以用线性时间解决。我们假象一个团队决斗比赛，队内不能决斗，只能一一决斗。两人决斗结果只有一换一，决斗两人都退场。如果有一个队伍成员超过半数，那么最后赢得肯定是这个队。

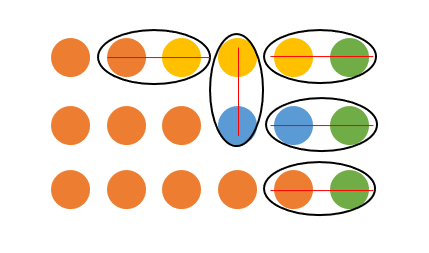
我们得出的算法就是这样：

element_type find_mojority_elem(element_type A[], int n)
{
  element_type current;
  int counter = 0;

  for (int i = 0; i < n; i++) {
    if (counter == 0) {
      current = A[i];
      counter++;
    } else if (A[i] == current) {
      counter++;
    } else {
      counter--;
    }
  }

  return current;
}

算法很简单，时间复杂度 \( O(n) \) 常量空间。实际根本没人会去解决这种问题。但这个问题的通用版本却大有用途。

高频元素问题 (heavy hitters) ，是指从长度 \( n \) 的数组 \( A \) 中找到出现次数至少是 \( \frac{n}{k} \) 的元素。例如， \(k=10\) 指的是找到出现频率是总数的 \( 10 \% \) 以上的元素。

显然最多有 \( k \) 个这样的元素，最少一个这样的元素都没得。多数派问题中 \( k=2 \) 并且保证多数派元素必定存在。

高频元素问题常常出现再互联网时代，列举一些例子：

1. 电商网站计算热门商品。
2. 搜索网站计算热搜 (热门搜索词)。
3. 网络交换机识别高流量TCP流。
4. 计算热门页面。

一个明显的算法是，一轮扫描给 \( A \) 每个元素计数，然后输出计数超过 \( \frac{n}{k} \) 的元素，这样太浪费内存了。也可以先给 \( A \) 排序，再一次扫描输出现次数超过 \( \frac{n}{k} \) 的元素，这样还得排序。数据量大的话 \( A \) 都不能整个放到内存里，这两个办法都不太行。

那么，有没有只要一次遍历，还省内存的算法呢？

绝无可能！

解决高频元素问题，避不开另一个问题：某个元素是否在某个集合内？哈希表、树之类的数据结构免不了的，不然就得 \( O(n^{2}) \) 了。

算法设计大失败，赶紧夹着尾巴滚回家，躺到床上嘤嘤嘤吧！

仔细回顾高频问题的提出，精确的结果确实很难，需要大量的计算或者大量的内存，时间换空间或者空间换时间不停纠结，让人烦躁。不过，如果我们给出近似解，有没有意义呢？我们把问题修改为 \( \epsilon - HH \) 问题 ( \( \epsilon - \) approximate heavy hitt4ers problem)：

输入长度为 \( n \) 的数组 \( A \) 和参数 \( k \) 和 \( \epsilon \) ，要求输出一个列表，使得：

1. 数组 \( A \) 中出现至少 \( \frac{n}{k} \) 次的元素都在输出列表里。
2. 输出列表里所有元素在数组 \( A \) 中出现至少 \( \frac{n}{k} - \epsilon n \) 次。

如果 \( \epsilon =0 \) 就是高频元素问题了。如果 \( \epsilon = \frac{1}{2k} \) ，那么出现 \( \frac{n}{k} \) 次的都被统计输出，输出的结果里可能有一些出现至少 \( \frac{n}{2k} \) 次的元素。这个问题仍然很有意义。

解决近似高频元素问题的方法挺多的：

• Finding repeated elements
• Interpreting the Data: Parallel Analysis with Sawzall
• count-min sketch

接下来讲的小数据结构解决这个问题，名为 count-min sketch，因为它足够简单，而且被应用到了现实世界。 AT&T 在网络交换机使用这个数据结构分析网络流量。 Google 在 MapReduce 上也实现了类似的算法，来做日志分析。

如果你了解 Bloom-Filter，或者有损压缩，这个数据结构很容易理解，没听过也没有关系。

count-min-sketch (CMS) 支持两个操作： \( Inc(x) \) 和 \( Count(x) \) 。 \( Count(x) \) 表示 \( x \) 出现的频次，也就是 \( Inc(x) \) 被调用的次数。

整个结构是个 \( l \) 行 \( b \) 列的数组 \(CMS\) ，\( b \) 表示哈希桶个数， \( l \) 表示哈希函数个数。通常 \( b \) 约为上千，\( l \) 不超过10。

两个操作分别为：

Inc(x) ：

\[ for i= 1,2,\cdots ,l: \\ \quad ++CMS[i][h_{i}(x)] \]

Count(x) :

\[ return \quad min^{l}_{i=1}CMS[i][h_{i}(x)] \]

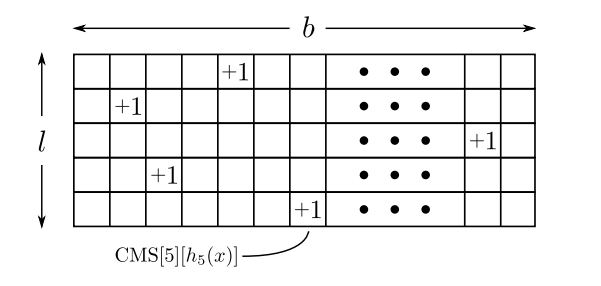
两个操作时间复杂度都是 \( O(l) \) 。这个数据结构只可能高估频率，不会低估。高估的多少，以及概率取决于 \(b\) 和 \(l\) 。如果 \(b\) 增大，就减少哈希冲突；如果 \(l\) 增大，就计算更多估值，得到更可靠的结果。

如果只想要搞懂数据结构，后面误差分析的内容可以跳过了。

误差和参数 \( b \) 、 \(l\) 有什么关系？

简单起见，我们先考虑 \(CMS\) 中一行的计数。考虑元素 \(x\) ，如果运气好，没有哈希冲突， \( f_{x} = CMS[i][h_{i}(x) \) 就是 x 的实际频次。如果运气不好，其它一些元素 \(y\) 的哈希值和 \(x\) 冲突了，那么 \(y\) 出现的频次 \(f_{y}\) 也被加到 \(CMS\) 数组上：

\[ CMS[i][h_{i}(x)] = f_{x} + \sum_{y\in S}f_{y} \]

其中 \( S=\{ y\neq x: h_{i}(y)=h_{i}(x)\} \) ，表示哈希值和 \(x\) 冲突集合。\(f_{x}\) 和 \(f_{y}\) 是常量，\(S\) 取决于哈希函数 \( h_{i}\) 的选择。

元素 \(x\) 与其他元素，大概有 \(\frac{1}{b}\) 的概率冲突，所以我们估计：

\[ CMS[i][h_{i}(x)] = f_{x} + \frac{1}{b} \sum_{y\neq x}f_{y}\leq f_{x}+\frac{n}{b} \]

期望高估 \(frac{n}{b}\)。在 \(n\) 大概几十亿，\(b\) 约一万的场景，这个误差应该可以接受。注意我们现在只是在\(CMS\)数组的一行上分析。

我们假设对与任意两个元素 \(x\) 和 \(y\) ，有 \( \mathbb{P}[h_{i}(y)=h_{i}(x)]\leq \frac{1}{b} \)。令

\[ Z_{i} = f_{x}+\sum_{y\neq x}f_{y}1_{y} \]

其中当哈希冲突时， \(1_{y}=1\) ，否则 \(1_{y}=0\) 。其期望不大于 \(\frac{1}{b}\)，因此

\[ E[Z_{i}]\leq f_{x}+\frac{1}{b} \sum_{y\neq x}f_{y} \leq f_{x}+\frac{n}{b} \]

令 \(X=Z_{i}-f_{x} \geq 0\) 表示误差， \( b=\frac{e}{\epsilon} \) (这是为了方便计算)，那么期望误差 \(X\) 为 \( \mathbb{E}[X]=\frac{\epsilon n}{e} \) 。根据马尔可夫不等式：

\[ \mathbb{P}[X>c\cdot \mathbb{E}[X]] \leq \frac{1}{c} \]

得

\[ \mathbb{P}[X>e\cdot \frac{\epsilon n}{e}]\leq \frac{1}{e} \]

因此

\[ \mathbb{P}[Z_{i} > f_{x}+\epsilon n] \leq \frac{1}{e} \]

假设哈希函数都是各自独立得，那么

\[ \mathbb{P}\left[\min_{i=1}^{l} > f_{x}+\epsilon n \right] = \prod _{i=1}^{l} \mathbb{P}[Z_{i} > f_{x}+\epsilon n] \leq \frac{1}{e^{l}} \]

误差概率为 \(\delta = \frac{1}{e^{l}} \)，只需要令 \( l \geq \ln\frac{1}{\delta} \) 即可。如果要让误差概率大概为 \(1\% \)，令 \(l=5\) 是足够的。