记录历史:持久化数据结构
Table of Contents
文本编辑器里的 "undo" 和 "redo",数据库系统的 MVCC,git 的历史记录,mac 的 Time Machine,等等功能,他们都有一个共同点,就是记录历史。这个功能依赖一种数据结构:持久化数据结构 (Persistent data structure)。持久化数据结构记录所有历史版本,你可以读取任意版本的数据。
1. "持久化" 的含义
"持久化(persistence)" 是指拥有查询数据历史版本的能力,它有以下4个级别:
- 半持久化 (Partial Persistance) - 可以读数据结构过去任意版本,只能在最新版本写。
- 全持久化 (Full Persistance) - 可以读数据结构过去任意版本,可以在数据结构任意版本写。
- 可合并持久化 (Confluent Persistent) - 不光可以在任何版本上读写,还可以将两个版本合并以创建一个新的版本。
- 函数式持久化 (Functional Persistance) - 函数式编程中实现的持久化数据结构,对象都是只读的,任意修改都是创建一个新的节点,而不是在旧节点上修改。参考 Puerly functional data structure。
以上四种持久化是逐步增强的,函数式持久化包含可合并持久化,合并持久化包含全持久化,全持久化包含半持久化。函数式持久化包含合并持久化是因为在函数式持久化中我们只限制了实现方式。如果在合并持久化中我们不允许合并,那么它就是全持久化。在全持久化中限制只能在最新版本上写,它就变成了半持久化。
4种持久化示意图如下所示。
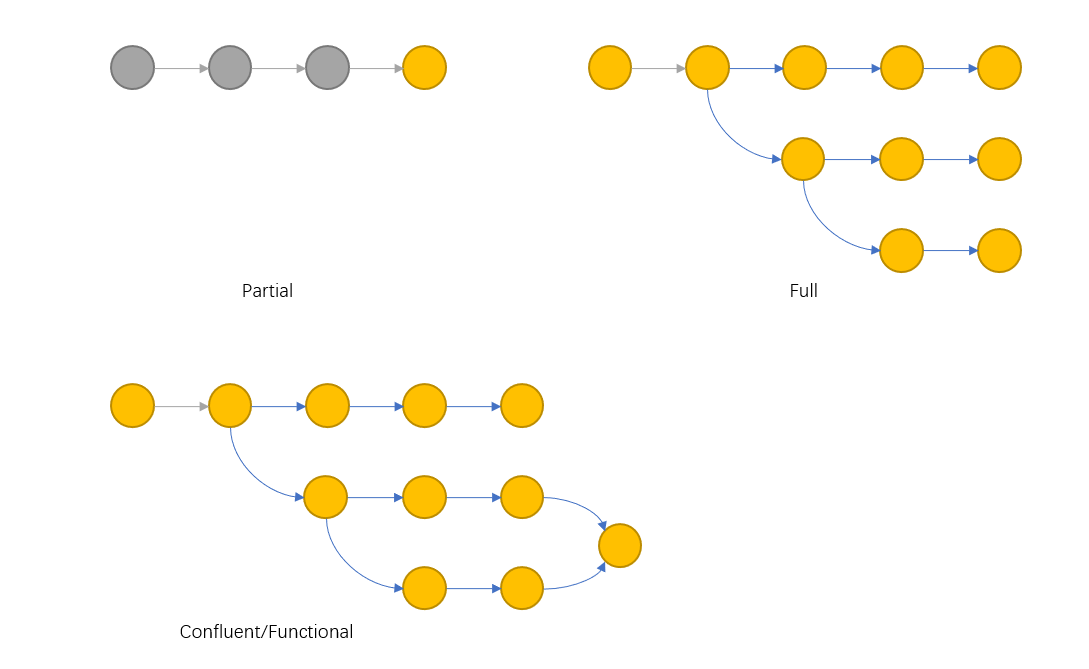
Figure 1: 持久化级别示意图
半持久化就像是 undo 和 redo,它是线性的记录历史。 全持久化就像是 emacs 上的 undo-tree,它记录了分支。合并持久化就像是 gitflow,它允许分支与合并操作。
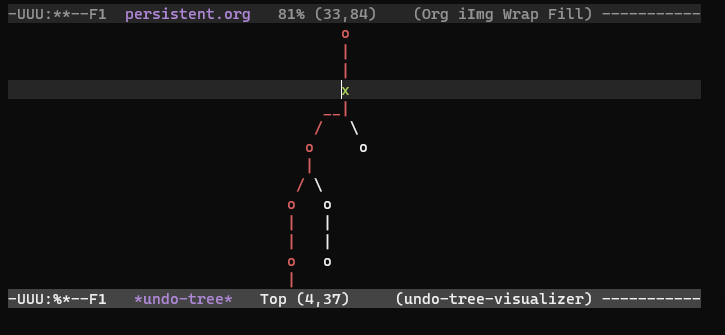
Figure 2: emacs undo-tree
Figure 3: gitflow
2. 半持久化数据结构
先看半持久化链表的实现,很容易扩展出其他数据结构半持久化版本。
2.1. 半持久化链表的实现方法
正常链表节点包含三个成员: (val, next, prev), val 表示节点值,next 指向链表下一个节点, prev 指向链表上一个节点。 要实现半持久化,还需要一个区域 mods,用来保存节点的修改历史。
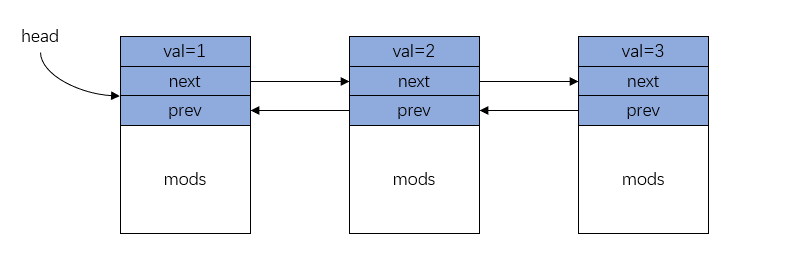
(1) 写操作, new_version = write(node, variable, value)
半持久化写操作参数为变量,目标值,返回版本号。
如果节点 n 的 mods 区域没有满,还能容纳新的修改历史,就把修改历史直接写到
mods 区域。
如果节点 n 已经的 mods 区域已经写满了,再也不能容纳新的修改历史了:
- 新建节点
n'。 - 将节点
n的最新值 (包括 val, next, prev) 复制到n'。 - 对所有
n指向的节点x(x=n->next),修改反向指针指向n'(x->prev=n')。 - 对于所有拥有指针指向
n的节点x(x->next=n),递归的调用write(x, next, n')。
(2) 读操作, read(node, variable, version)
读操作 read(node, var, v) 查询 mods 记录,找到版本最大的记录版本 \(w\) 使得
\(w\leq v\) , 版本修改记录 \(w\) 中的值就是要查询的值。
以上述链表为例,要修改第二个节点 v1=write(node2, val, 20) ,只需要添加 mods 修改历史,如图所示。
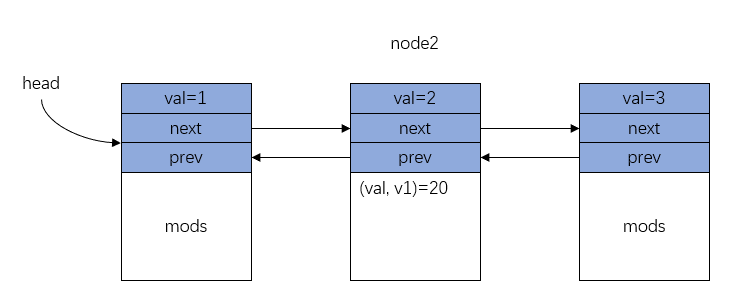
Figure 4: 持久化链表接结构示意图
再多加几次修改:
v2=write(node2,val,33) v3=write(node2,val,50) v4=write(node2,val,21)
结构如下图, mods 区域已经写满了。
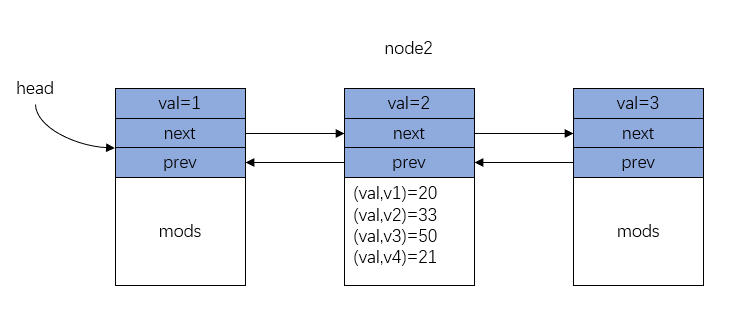
Figure 5: 持久化链表 - 节点满
记没修改过的初始值为 v0 。要查询这个链表 v3 版本,从根节点开始: (val,v0)=1,(next,v0)=node2 ; node2
节点查询到满足 \(\leq v3\) 的版本 (val,v3)=50,(next,v0)=node3,(prev,v0)=node1 ;
node3 节点查询到满足 \(\leq v3\) 的版本
(val,v0)=3,(next,v0)=nullptr,(prev,v0)=node2 。得知链表在版本 v3 为
<1,50,3> 。
再修改 node2 的值 v5=write(node2,val,200) ,此时 mods 已经满了,需要新建节点 new_node2 :
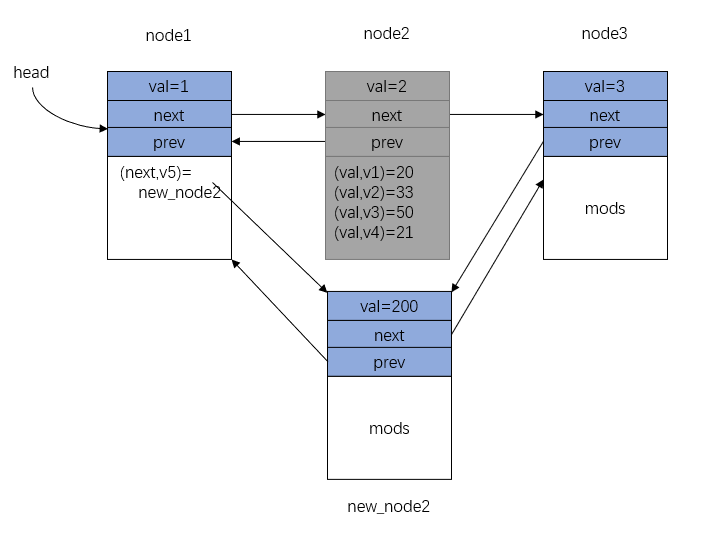
Figure 6: 持久化链表 - 新建节点
此时查询链表版本 v5 , 从根节点开始: (val,v0)=1,(next,v5)=new_node2 ; new_node2
节点 (val,v0)=200,(next,v0)=node3 , node3 节点 (val,v0)=3,(next,v0)=nullptr
。得知链表版本 v5 为 <1,200,3> 。
不难看出如果 write() 方法要递归修改多处,均修改完成后返回版本的最大值。
使用类似的方法,可以实现半持久化二叉树等数据结构。 基本数据结构都可以使用节点和指针来表示,稍作变化就可以半持久化几乎所有基本数据结构。
2.2. 更一般的半持久化数据结构
链表、树、图可以抽象为 Pointer Machine 。我们扩展 Pointer Machine,将其变成半持久化数据结构,这样就相当于扩展了任意基础数据结构。
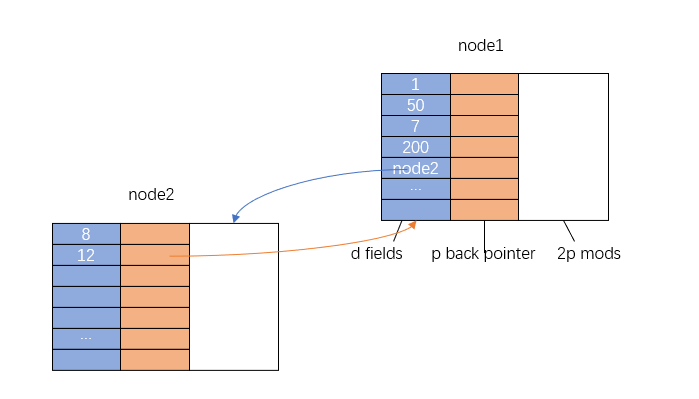
Figure 7: pointer machine 持久化结构
只考虑入度确定的 Pointer Machine,设入度为 \(p\) , 如上图所示,每个节点有三类成员。
- 只读的数据成员,共 \(d\) 个数据成员。 这是原有数据结构本来就存在的,数据成员包括数值和指针。
- 可写的反向指针区域 (back pointers)。这些反向指针能告诉我们哪些节点的数据成员指向了当前节点。入度是 \(p\) 所以反向指针成员数量为 \(p\) 。
- 可写的修改历史区域 (
mods)。保存对节点数据成员的修改,内容结构是(field,version)=value。注意修改反向指针并不需记录mods。
实现任意节点的读写操作如下:
read(node, field, version)- 在节点的修改记录区node.mods查找修改field成员的最大版本 \(w\) , 使得 \(w\leq version\) 。 如果没找到,那么只读的数据成员区域的field成员就是当前值。write(node, field, value)- 如果node.mods没满,就向其中添加一个记录(field,version)=value。如果node.mods满了:- [新建节点]
node' - [设置最新值] 将旧节点的数据成员区域(数据和指针)的最新值复制到
node'的数据成员区域。 - [修改其他节点的反向指针] 任意
node指向的节点x, 修改x的反向指针指向新节点node'。 - [递归修改其他节点的指针成员] 任意指向
node的节点x, 递归调用write(x, pointer_to_node, node')使得最新版本的指针指向新节点。
- [新建节点]
演示半持久化二叉树实现如下图。
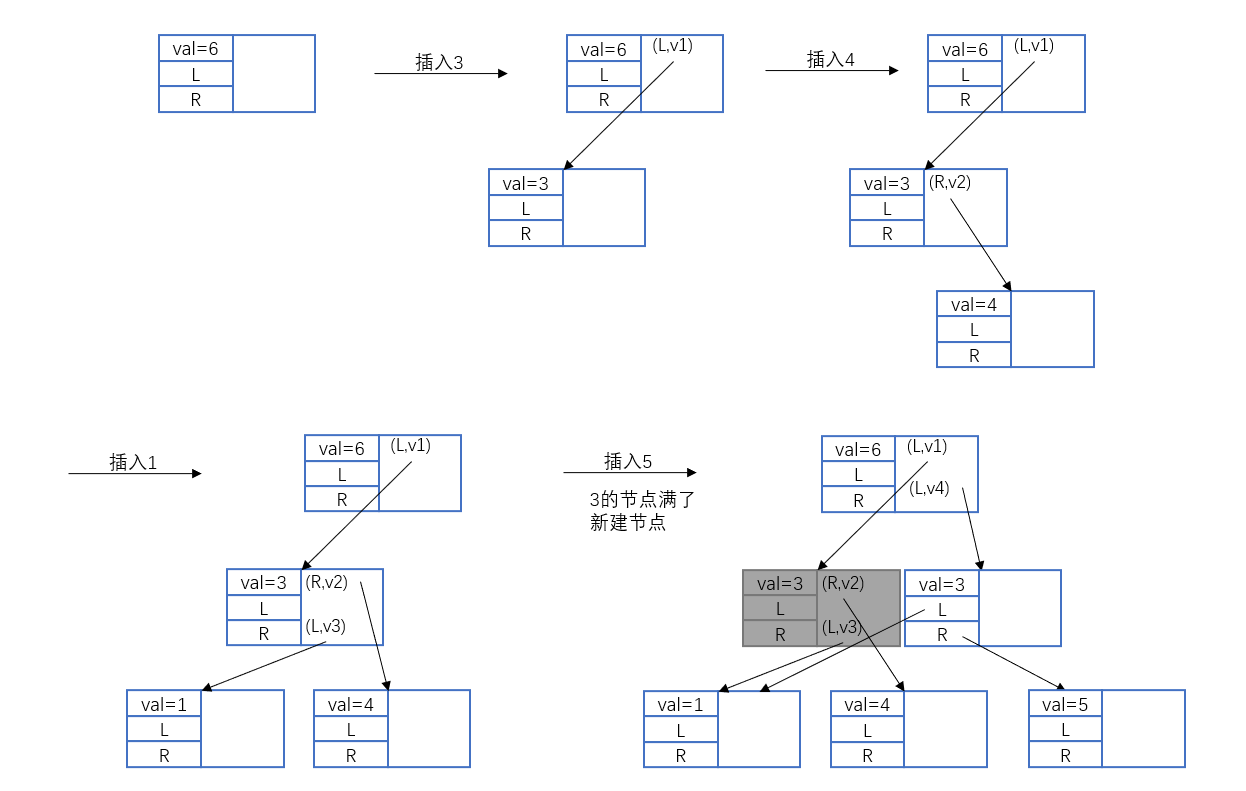
Figure 8: 半持久化二叉查找树
2.3. 半持久化数据结构的时间复杂度
我们只考虑度数是指定常数的数据结构。节点入度数为 \(p\) , 令节点的 mods 的最大记录数量为 \(2p\) 。
读操作 read(node, field, version) 是很快的,只需要读取 node.mods , \(O(1)\) 。写操作 write(node, field, value) 有两种情况,如果节点没满,直接写入一个修改日志,复杂度是 \(O(1)\) ; 如果节点满了,可能会递归调用 write() 修改指针:
\[ cost(n) = c + \sum_{all\ node\ x\ point\ to\ n}\left(cost(x)\right) \]
其中 \(c\) 表示新建一个节点并复制旧节点数据,修改反向指针的 \(O(1)\) 操作。递归步骤是很贵的,但只有节点满的时候才会执行递归操作,然后节点又会变空,直到节点变满之前都不会引起递归操作。平均下来 write() 耗时很少。 我们使用摊还分析
(amortize analysis) 来计算写操作的事件复杂度。
设势能函数 \(\phi\) , 每次操作的摊还代价等于这次操作的实际代价加上此操作引起的势能变化:
\[ amortized\_cost(n) = cost(n) + \Delta\phi \]
势能函数为:
\[ \phi = c\times (mods\ number) \]
节点之前是满的,后来空了,所以势能变化为 \(-2cp\) 。
\[ amortized\_cost(n) \leq c + c - 2cp + p \times amortized\_cost(x) \]
对于节点 \(x\) , 公式中第二个 \(c\) 是找到 mods 对应位置并添加个记录的次数,所以造成势能增加 \(c\) 。
将右边展开容易的出均摊复杂度是 \(O(1)\) 。 更详细的分析见此文档。
3. 全持久化数据结构
3.1. 全持久化版本号的问题
在半持久化数据结构中,版本是线性的、全序的,版本号使用数字就可以,数字大小表现了版本的新旧关系。全持久化可以修改任意版本,它的版本变化形成树形结构,版本是个偏序关系,并不是任意两个版本都可以比较的。如下图,版本 \(a\) 和版本 \(b\) 的关系是 \(a < b\) ,但版本 \(b\) 和版本 \(d\) 是不可比较的。因此版本使用数字大小来代表就不合适了,全持久化中的版本只是一个标识,他的序关系只能在版本树中展示,这意味着每次比较版本号都执行一个 \(O(n)\) 操作。
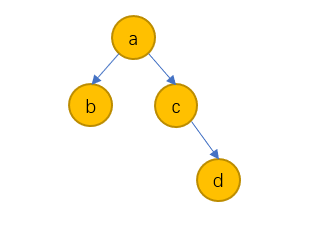
Figure 9: 全持久化数据结构版本树
幸运的是,树形结构可以通过中序遍历的顺序转化为线性结构,中序遍历过程中记录每个节点初次访问和末次访问的顺序。如上图的树,线性表示为:
\[ b_{a}b_{b}e_{b}b_{c}b_{d}e_{d}e_{c}e_{a} \]
\(b_{a}\) 表示初次访问节点 \(a\) , \(e_{a}\) 表示末次访问节点 \(a\) 。这样,就很容易判断后继、前序的关系,例如 \(b_{c}>b_{d}>e_{d}>e_{c}\) 可知 \(d\) 是 \(c\) 的后继。有一个数据结构 order maintenance 可以在 \(O(1)\) 的时间复杂度上实现这个版本号序的解答。这样就可以在 \(O(1)\) 时间内解答版本 \(v\) 是否是版本 \(w\) 的后继。
3.2. 全持久化数据结构实现
如下图所示,全持久化的数据结构与半持久化数据结构类似。同样值考虑入度为 \(p\) 的数据结构。每个节点存储 \(d\) 个成员 (包括数据和指针), \(p\) 个反向指针, 注意出度也受到成员数量 \(d\) 的限制。 mods 区域大小增加到 \(2(d+p+1)\) , mods 除了保存数据成员的修改,也要保存反向指针的修改。
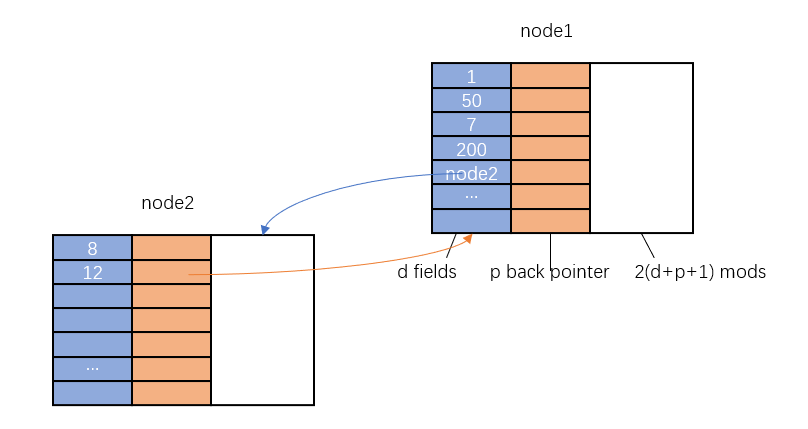
Figure 10: 全持久化 pointer machine 结构示意图
实现读写操作如下。
read(node, field, version)- 在mods中使用 order-maintenance 结构找到 \(version\) 或它的最近前驱,返回其值。write(node, field, value, version)- 如果node.mods还有空间,就添加一个记录(field,version_next)=value, 其中 \(version_next>version\) 。如果node.mods满了:- [以版本 \(k\) 为界切分子树] 新建节点 \(m\) 。将节点 \(node\) 的
mods记录分为两份,使得存在某个版本 \(k\) 和它的的所有后继都在其中一份,另一份中不包含 \(k\) 或任何 \(k\) 的后继。新节点 \(m\) 保存所有 \(k\) 的后继的mods;老节点 \(node\) 保存其它的。如下图所示。 - [保存版本 \(k\) 的值] 计算老节点 \(node\) 的最近 \(m\) 的前驱版本所有数据和反向指针,复制到 \(m\) 的数据区。
- [修改指针] 递归调用
write()更新所有邻居的指针(正向和反向),最多需要更新 \(d+p+(d+p+1)\) 次。
- [以版本 \(k\) 为界切分子树] 新建节点 \(m\) 。将节点 \(node\) 的
3.3. 全持久化数据结构的时间复杂度
显然读操作复杂度是 \(O(1)\) 。
写操作如果不切分节点的话是 \(O(1)\) , 如果要切分节点就比较复杂。同样使用 amortize 技术:
\[ \phi = -c(numer\ of\ empty\ mods) \]
势能函数是 mods 空间数量的负数(其实每次操作的势能变化都加上 mods 空间总量就是 mods 记录数,与半持久化时一样)。 如果切分 \(\Delta\phi = -2c(d+p+1)\) 否则
\(\Delta\phi=c\) 。所以
\[ amortized\_cost(n) \leq c + c - 2c(d+p+1)+(d+p+(d+p+1))*amortized_cost(x) \]
展开后常数部分消失了,所以写操作是 \(O(1)\) 。
4. 合并持久化数据结构
实现方法可以参照以上全持久化数据结构。版本从树结构变成了有向无环图,但是偏序关系仍在。
合并操作很麻烦,比如说某个版本,自己跟自己合并, 合并后的新版本再跟自己合并,这样合并 \(n\) 次之后版本就有 \(2^{n}\) 了。
可合并持久化数据结构的时间复杂度分析很麻烦,每种特定的数据结构可以定义自己的合并操作,就可能出现不同的时间复杂度。 具体参考 Making Data Structures Confluently Persistent。
5. 函数式持久化数据结构
相比与前述结构,它只规定了使用函数式方法来实现。有几个成熟的数据结构实现了函数式持久化:
二叉树 (Functional balanced BST) - 主要是复制一份要修改的节点,并把它的前驱节点都复制一份因为要修改。 Confluently Persistent Tries for Efficient Version Control 这篇文章实现了 \(O(log(n))\) 的函数式持久化实现。
#+CAPTION 函数式持久化二叉树
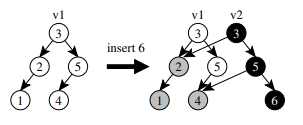
- 列表 - Purely Functional Worst Case Constant Time Catenable Sorted Lists 实现了这个数据结构的函数式持久化。
可以参照这几个数据结构实现函数式持久化的其他数据结构。