关于二分查找算法

1. 传统二分查找
2. 中途不退出二分查找
3. upper bound
4. lower-bound
5. Knuth 的二分查找
6. 指数查找
7. 比例二分查找

二分查找，也叫 binary search，half-interval search，logarithmic search， binary chop，是在可随机寻址的有序列表中根据元素的值查找元素的位置的算法。它拥有和排序二叉树相似的查询效率，也就是 \(O(\log n)\) 的时间复杂度。通俗的讲，在一个长度为 \(n\) 的有序序列表中查询一个元素的位置，只需 \(a\log(n) + c\) 次比较操作，其中 \(a\) 和 \(c\) 是常量。通常情况下，二分查找的空间复杂度是 \(O(1)\) 。它的特点是效率好，容易写，容易写错。

二分查找每次取区间中的中间值和目标值比较，如果目标值较大，则中间值及其左边的所有元素都比目标值少，都排除出区间，在新的区间中继续查找；如果目标值较小，则中间值及其右边的所有元素都比目标值大，都排除出区间，在新的区间中继续二分查找。这样，每一轮迭代都可以减少一半的元素，效率非常高。

二分查找查找逻辑简单，应用广泛，变种很多，错误的变种也很多。这里将列举常见的变种，并细数我在工作遇到的各种错误。这里也会介绍一种分析二分查找的错误的简便方法。

1 传统二分查找

1.1 算法描述

传统二分查找每次迭代都比较区间中的中间值和目标值

(1) 如果中间值偏小，说明中间值及其左边的值都比目标值小，全部剔除出列表，继续下一轮迭代；
(2) 如果中间值偏大，说明中间值及其右边的值都比目标值大，全部剔除出列表，继续下一轮迭代；
(3) 如果中间值与目标值相等，则已经找到，中间点就是目标值的位置。
(4) 如果列表为空，说明整个列表中都没有与目标值相等的元素。

算法的实现代码如下：

/* search T in array A witch contain n elements, and return index of T.
 * Return -1 if T not exists in A. */
int binary_search(int *A, int n, int T) {
    int L = 0;
    int R = n - 1;
    int m = -1;
    while (L <= R) {
        m =  (L + R) / 2;
        if (A[m] < T)
            L = m + 1;
        else if (A[m] > T)
            R = m - 1;
        else
            return m;
    }
    return -1;
}

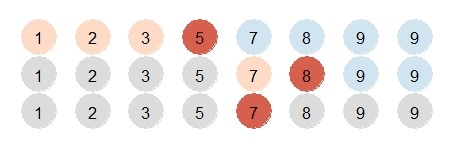
以在列表 {1,2,3,5,7,8,9,9} 中查找 7 为例，如下图所示，

第一轮迭代，列表为 {1,2,3,5,7,8,9,9}，中间值是5，比7小，剔除5及左边所有元素；
第二轮迭代，列表为 {7,8,9,9}，中间值是8，比7大，剔除8及右边所有元素；
第三轮迭代，列表为 {7}，中间值是7，找到结果，算法结束。

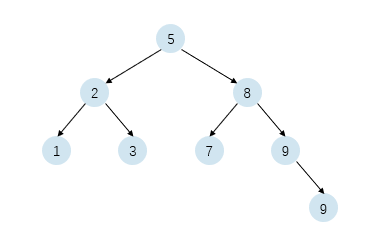
二分查找运行过程与在二叉排序树中查找某个元素类似。如果将上述例子中每个元素的查找过程逐一列举，则中间节点的轨迹与一棵二叉排序树是一样的：

显然，传统二分查找的准确性要求初始化，过程中以及结束时要保持如下断言：

编号	断言
1	每次迭代，要么使算法结束，要么列表中减少至少一个元素
2	每次缩短列表，不能删除任何目标值
3	找到目标值或者列表为空时结束

我们可以运用这些断言验证算法的正确性，比如上面的代码把if-else分支语句写反了，就违反断言2，肯定就错了。在比如初始化是就将R=n-2，那肯定将最后一个节点提出了，违反断言2，就是错了。

下面我们利用这些断言分析一些逻辑上常见的错误。

1.2 过早退出的错误

int binary_search(int *A, int n, int T) {
    int L = 0;
    int R = n - 1;
    int m = -1;
    while (L < R) { // 应该是 L <= R
        m =  (L + R) / 2;
        if (A[m] < T)
            L = m + 1;
        else if (A[m] > T)
            R = m - 1;
        else
            return m;
    }
    return -1;
}

观察这个程序，L指向列表第一个节点，R指向列表最后一个节点，L=R表示列表中仅包含一个节点。程序在L=R时即退出返回，不满足断言3，所以是错的。

以在列表 {1,2,3,5,7,8,9,9} 中查找 7 为例，

第一轮迭代，列表为 {1,2,3,5,7,8,9,9}，中间值是5，比7小，剔除5及左边所有元素；
第二轮迭代，列表为 {7,8,9,9}，中间值是8，比7大，剔除8及右边所有元素；
第三轮迭代，列表为 {7}，循环退出，返回-1。

这个结果显然是错误的。

1.3 无法退出的错误

int binary_search(int *A, int n, int T) {
    int L = 0;
    int R = n - 1;
    int m = -1;
    while (L <= R) {
        m =  (L + R) / 2;
        if (A[m] < T)
            L = m; // 应该为 L=m-1
        else if (A[m] > T)
            R = m - 1;
        else
            return m;
    }
    return -1;
}

这个程序不满足断言 1。以在列表 {1,2,3,5,7,8,9,9} 中查找 4 为例，

第一轮迭代，列表为 {1,2,3,5,7,8,9,9}，中间值是5，比4大，剔除5右边所有边所有元素；
第二轮迭代，列表为 {1,2,3}，中间值是2，比4小，剔除2左边所有元素，不剔除2；
第三轮迭代，列表为 {2,3}，中间值是2，比4小，剔除2左边所有元素，没有剔除2；
第四轮迭代，列表为 {2,3}，中间值是2，比4小，剔除2左边所有元素，没有剔除2；
第n轮迭代，列表为 {2,3}，中间值是2，比4小，剔除2左边所有元素，没有剔除2；

这样程序在列表 {2,3} 中循环，不能结束，所以这个算法是错误的。

类似的，下面的算法也是一样的错误

int binary_search(int *A, int n, int T) {
    int L = 0;
    int R = n - 1;
    int m = -1;
    while (L <= R) {
        m =  (L + R) / 2;
        if (A[m] < T)
            L = m - 1;
        else if (A[m] > T)
            R = m; // 应该为 R = m - 1;
        else
            return m;
    }
    return -1;
}

这个算法不满足断言1，不能从列表 {2,3} 查找1这个循环中退出。

1.4 剔除目标值的错误

int binary_search(int *A, int n, int T) {
    int L = 0;
    int R = n - 1;
    int m = -1;
    while (L <= R) {
        m =  (L + R) / 2;
        if (A[m] <= T) // 应该为 if (A[m] < T)
            L = m + 1;
        else if (A[m] > T)
            R = m - 1;
        else
            return m;
    }
    return -1;
}

修改的那一行会将目标值剔除，不满足断言2。所以是错误的。

考虑从{2,3}中查找2，中间值是2，满足 A[m] <= T，2及其左边所有元素剔除，列表为 {3}。下一轮迭代，将3剔除，列表为空，算法退出，返回 -1。

将

else if (A[m] > T)

修改为

else if (A[m] >= T)

也是同样的错误。

1.5 整型溢出的错误

可能有的人注意到计算中间值的那一行代码有整形溢出的风险。数组长度确实可能超过2G，可能会溢出。这么写是为了保持代码简单，在实际工作中使用这样的代码是错误的。修改方法如下：

// 加法有整型溢出风险
m = (L + R) / 2;

// 第一种修改方法
// 使用符号位保存溢出的比特位，在除以2之后符号位一定会是0。
// 这种写法使用一次加法，一次除法
m = (int)(((unsigned int)L + (unsigned int)R) / 2);

// 第二种修改方法
// 利用恒等式 (L+R)/2 = L+(R-L)/2
// 将可能溢出的加法变换为不会溢出的加法。不会溢出是因为
// L+(R-L)/2 < R
// 这种写法使用一次加法，一次减法，一次除法
m = L + (R - L) / 2；

// 有的人会将 a/2 替换为 (a >> 1)
// 常用于右移指令比除法快的架构中，常见架构都是如此。
// 要注意 >> 运算符优先级低于 +-*/ 四则运算，需要括号。
m = L + ((R - L) >> 1);

2 中途不退出二分查找

传统二分查找每轮迭代都要比较中间值是否和目标值相等，一些算法实现可以去掉这个判断。这个算法只有在列表中仅剩一个节点时判断是否与目标值相等，每轮可以减少一次比较，但是平均会增加一轮迭代。Hermann Bottenbruch 在 1962 年发表了第一个这种实现，转换成了C语言如下：

/* search T in array A witch contain n elements, and return index of T.
 * Return -1 if T not exists in A. */
int binary_search_less_compare(int *A, int n, int T) {
    int L = 0;
    int R = n - 1;
    int m = -1;

    if (n <= 0)
        return -1;

    while (L < R) {
        m = (L + R + 1) / 2;
        if (A[m] > T)
            R = m - 1;
        else
            L = m;
    }

    if (A[L] == T)
        return L;
    return -1;
}

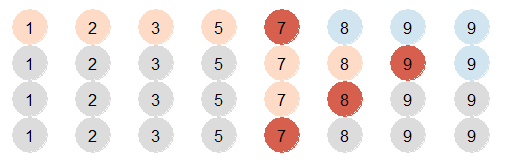
以在列表 {1,2,3,5,7,8,9,9} 中查找 7 为例，如下图所示，

第一轮迭代，列表为 {1,2,3,5,7,8,9,9}，中间值是7，不比目标值7小，剔除7左边的元素；
第二轮迭代，列表为 {7,8,9,9}，中间值是9，比7大，剔除9及右边所有元素；
第三轮迭代，列表为 {7,8}，中间值是8，比7大，剔除8以及右边所有元素；
最后列表为 {7}，仅剩一个元素，循环退出，判断中间值与目标值相等，列表地址，也就是7的地址，算法退出。

这个算法与传统二分查找相比，有以下几点不同：

中途不退出二分查找使用中间或中间偏右的元素为中心节点，而传统二分查找以中间或中间偏左的元素为中心节点。
中途不退出二分查找在仅剩一个元素时退出迭代，而传统二分查找在中间元素与目标值相等或者列表为空时退出。
中途不退出二分查找在迭代中减少了一轮比较。
中途不退出二分查找使用 L=m 而不是 L=m-1。
中途不退出二分查找在循环结束时需要一次比较。
为了防止未定义行为，上述程序在开始处添加了列表为空的判断。

这个算法遵守的断言如下：

编号	断言
1	每次迭代，列表中减少至少一个元素
2	每次缩短列表，不能删除任何目标值
3	列表至少包含一个元素

明明使用 L=m，为什么还能满足断言1呢？

这是因为m不可能是目标值的地址。每次迭代条件L<R保证了列表中至少有两个元素。如果列表中元素有3个或者3个以上，m不会是列表边界，肯定能减少元素。如果列表中有2个元素， m 肯定指向右边的那个元素，此时L=m也肯定能减少一个元素，所以无论什么情况，都满足断言1。

这个算法也经常被写错，下面选一些常犯的错误进行分析。

2.1 晚退出的错误

int binary_search_less_compare(int *A, int n, int T) {
    int L = 0;
    int R = n - 1;
    int m = -1;

    if (n <= 0)
        return -1;

    while (L <= R) { // 应该是 L<R
        m =  (L + R + 1) / 2;
        if (A[m] > T)
            R = m - 1;
        else
            L = m;
    }

    if (A[L] == T)
        return L;
    return -1;
}

上面的循环在列表为空时才退出，违反了断言3。这可能令算法进入死循环无法退出。

例如，从 {3} 中查找 3，进入循环，A[m]>T 不成立，L=m，列表仍然为 {3}，又回到了原始问题，进入了死循环。

2.2 中间偏左的错误

int binary_search_less_compare(int *A, int n, int T) {
    int L = 0;
    int R = n - 1;
    int m = -1;

    if (n <= 0)
        return -1;

    while (L < R) {
        m = (L + R) / 2; // 应该为 m = (L + R + 1) / 2;
        if (A[m] > T)
            R = m - 1;
        else
            L = m;
    }

    if (A[L] == T)
        return L;
    return -1;
}

这就违反了断言1了。例如在 {2,3}中查找2，在else分支中，2不会被删除，进入死循环。

如果硬要用中间偏左的元素，那应该写成下面这样：

int binary_search_less_compare(int *A, int n, int T) {
    int L = 0;
    int R = n - 1;
    int m = -1;

    if (n <= 0)
        return -1;

    while (L < R) {
        m = (L + R) / 2;
        // 因为m是中间偏左，为了保证至少剔除一个元素，
        // 要么至少 L=m+1，要么 R=m。
        if (A[m] < T)
            L = m + 1;
        else
            R = m;
    }

    if (A[L] == T)
        return L;
    return -1;
}

2.3 没有剔除元素的错误

int binary_search_less_compare(int *A, int n, int T) {
    int L = 0;
    int R = n - 1;
    int m = -1;

    if (n <= 0)
        return -1;

    while (L < R) {
        m = (L + R + 1) / 2;
        if (A[m] > T)
            R = m; // 应该是 R = m - 1;
        else
            L = m;
    }

    if (A[L] == T)
        return L;
    return -1;
}

因为m是中间偏右，R=m不能令列表缩小，违反了断言1。在{2,3}中查找1就会出现因为这个错误进入死循环。

2.4 剔除了目标值的错误

int binary_search_less_compare(int *A, int n, int T) {
    int L = 0;
    int R = n - 1;
    int m = -1;

    if (n <= 0)
        return -1;

    while (L < R) {
        m = (L + R + 1) / 2;
        if (A[m] > T)
            R = m - 1;
        else
            L = m + 1; // 应该是 L = m;
    }

    if (A[L] == T)
        return L;
    return -1;
}

如果m是目标值的地址，则进入else分支，执行 L=m+1 将目标值剔除。违反了断言2。怎么可能有人犯这种错误？

3 upper bound

3.1 算法描述

如果列表中有重复元素，查找目标值是否在列表中可能不太满足需求，这就产生了两个变种： upper bound 和 lower bound。

upper bound 是最常用的，它返回的是列表中第一个比目标值大的元素，也就是第一个插入位置。返回值总是目标值的插入位置，如果插入位置有值，则将该位置以及右边所有元素向右平移一次，再插入。

例如下面的列表，如果查找0，则返回0；如果查找1，则返回2；如果查找3，则返回3；如果查找4，则返回3。

地址	0	1	2
值	1	1	3

从需求可以分析出，每轮迭代中，

如果中间值等于目标值，可以将中间值及其左边的元素都剔除；
如果中间值大于目标值，也可以将中间值及其左边的元素都剔除；
如果中间值小于目标值，可以将中间值右边的元素剔除，不剔除中间值。

到最后，列表为空时，当前列表的起点就是要查找的地址。

为了令列表后的第一个节点可以到达，将列表后的第一个节点也加入到初始列表，他的值无所谓，因为根本不会对他寻址。为了方便理解，可以将其看作正无穷大。

int bs_upper_bound(int *A, int n, int T) {
    int L = 0;
    int R = n;
    int m = -1;
    while (L < R) {
        m = (L + R) / 2;
        if (T >= A[m]) {
            L = m + 1;
        } else {
            R = m;
        }
    }
    return L;
}

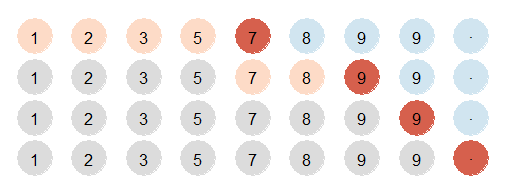
以在列表 {1,2,3,5,7,8,9,9} 中查找 9 为例，如下图所示，

第一轮迭代，列表为 {1,2,3,5,7,8,9,9,∞}，中间值是7，比目标值7小，剔除7左边的元素；
第二轮迭代，列表为 {7,8,9,9,∞}，中间值是9，剔除9及左边所有元素；
第三轮迭代，列表为 {9,∞}，中间值是9，剔除9；
最后列表为 {∞}，中间值是∞，比9大，将其剔除，列表为空，算法结束，此时当前列表的地址为列表后紧跟着的节点，将其返回。

显然，要正确实现 upper bound，需要满足以下断言：

编号	断言
1	每次迭代，列表中减少至少一个元素
2	除最后一轮迭代外，不能将目标值右边的元素剔除
3	列表为空时，算法结束
4	不能对n寻址，因为没有值

这个算法也有一些常犯的错误，下面选取一些逐个分析。

3.2 无法剔除元素的错误

int bs_upper_bound(int *A, int n, int T) {
    int L = 0;
    int R = n;
    int m = -1;
    while (L < R) {
        m = (L + R) / 2;
        if (T >= A[m]) {
            L = m; // 应为 L = m + 1;
        } else {
            R = m;
        }
    }
    return L;
}

这违反了断言1。例如，在 {1} 中查找1，一轮迭代结束后列表没有缩短，进入死循环。这显然是错误的。

3.3 剔除了目标值后面元素的错误

int bs_upper_bound(int *A, int n, int T) {
    int L = 0;
    Int R = n;
    int m = -1;
    while (L < R) {
        m = (L + R) / 2;
        if (T >= A[m]) {
            L = m + 1;
        } else {
            R = m - 1; // 应外 R = m;
        }
    }
    return L;
}

修改后的那一行使得算法违反了断言2。例如在 {1,3,4} 查找 1 时将 3 剔除，违反了断言 2，返回错误结果。

3.4 初始化错误

int bs_upper_bound(int *A, int n, int T) {
    int L = 0;
    int R = n - 1; // 应为 int R = n;
    int m = -1;
    while (L < R) {
        m = (L + R) / 2;
        if (T >= A[m]) {
            L = m + 1;
        } else {
            R = m;
        }
    }
    return L;
}

初始化 R=n 写成 R=n-1，将列表后的那一个节点剔除，违反了断言1，如果硬要R=n-1，循环条件应该写成 L<=R；

3.5 剔除条件错误

int bs_upper_bound(int *A, int n, int T) {
    int L = 0;
    int R = n;
    int m = -1;
    while (L < R) {
        m = (L + R) / 2;
        if (T > A[m]) {
            L = m + 1;
        } else {
            R = m;
        }
    }
    return L;
}

if (T >= A[m]) 写成了 if (T > A[m])，这令 T=A[m]的情况下不能剔除任何节点，违反断言1。

4 lower-bound

lower bound 算法与 upper bound 类似，它返回的结果是列表中第一个等于目标值的元素的地址，如果列表中没有目标值，那么它将返回大于目标值的第一个元素。

例如下面的列表，如果要查找0，则返回0；要查找1，则返回0；要查找2，则返回2；要查找3，则返回2；要查找4，则返回3。

地址	0	1	2
值	1	1	3

upper bound 和 lower bound 有一个附带的性质： upper bound - lower bound = 目标值的元素的个数。

int bs_lower_bound(int *A, int n, int T) {
    int L = 0;
    int R = n;
    int m = -1;
    while (L < R) {
        m = (L + R) / 2;
        if (T <= A[m]) {
            R = m;
        } else {
            L = m + 1;
        }
    }
    return L;
}

显然，lower bound 必须满足以下断言：

编号	断言
1	每次迭代，列表中减少至少一个元素
2	除最后一轮迭代外，如果列表中没有目标值，那么大于目标值的第一个节点不能剔除
3	列表为空时，算法结束
4	不能对n寻址，因为没有值
5	如果列表中有目标值，最左边的目标值不能剔除

常见的错误于 upper bound 类似，不在赘述。

5 Knuth 的二分查找

这是 Donald Knuth 在《The Art of Computer Programming》中发明的算法。在一些架构中，比如十进制计算机中，计算中间点的运算效率太低，就可以使用这种方法来优化。

Uniform Binary search 在查找之前，提前生成了一个表，用于高效的计算中间值。表中的数据如下：

\begin{align*} delta_0 &= \frac{n+1}{2} \\ delta_1 &= \frac{n+2}{4} \\ delta_3 &= \frac{n+4}{8} \\ delta_4 &= \frac{n+8}{16}\\ \cdots & \end{align*}

这样，中间值就可以查表找到，每一轮，中间值通过查表计算 \(i=i-delta_k\) 或 \(i=i+delta_k\) 就可以得到新的中间值。完整代码如下：

#define N 10
#define LOG_N 4
static int delta[LOG_N];

void make_delta(int N) {
    int power = 1;
    int i = 0;
    do {
        int half = power;
        power <<= 1;
        delta[i] = (N + half) / power;
    } while (delta[i++] != 0);
}

int unisearch(int *A, int T) {
    int i = delta[0]-1;  /* midpoint of array */
    int d = 0;

    while (1) {
        if (T == A[i]) {
            return i;
        } else if (delta[d] == 0) {
            return -1;
        } else {
            if (T < A[i]) {
                i -= delta[++d];
            } else {
                i += delta[++d];
            }
        }
    }
}

int main(void) {
    int A[N] = {1,3,5,6,7,9,14,15,17,19};
    make_delta(N);
    unisearch(A, 15);
    return 0;
}

除了 TAOCP 上的 MIX，我没有见过十进制计算机，所以很少见到这种实现。即使是十进制计算机，在没有确定性能瓶颈的情况下，也不会去优化，而性能瓶颈极少可能是因为二分查找的中间值消耗，估计以后也不会见到这种代码了。

算法实现的错误形式与之前提到的有相似的地方，因为没有人写过，不再分析了。

6 指数查找

指数查找先比较第 \(2^1\) 个元素，再比较第 \(2^2\) 个元素，再比较 \(2^3\) 个元素，一次类推，直到找到第一个大于目标值的地址为 \(2^k\) 的元素。迭代过程中会删除小的节点，找到第一个这样的元素后删除大的节点，在新的列表中继续执行指数查找过程。

以在列表 {1,2,3,5,7,8,9,9} 中查找 7 为例，查找过程如下图所示。

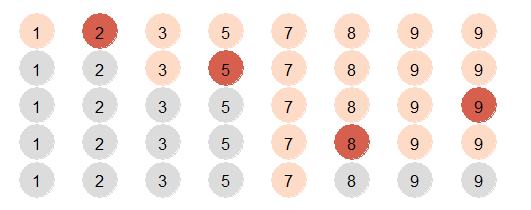
7 比例二分查找

比例二分查找不是每次取中心点作为中间值，而是根据一个算法选取中间值。

选取算法如下：

m = (T-A[L])/(A[R]-A[L]) * n;

如果列表够长，并且元素分布比较平均，比例二分查找比传统二分查找更快。元素分配平均或近似平均的情况下，时间复杂度可以达到 \(O(\log\log n)\) 。注意这不是最坏情况下的时间复杂度。

用量子算法来实现二分查找比传统计算机实现的时间复杂度要稍微好一点点，目前没有兴趣看，待更新吧。