对 CBC 模式的一些攻击
Table of Contents
我在超过10个土法炼钢项目里看到有问题 CBC 用法了。
Github 上有一个叫 crypto101 的项目,里面讲了很多经典的密码学话题,很有意思,这篇文章上的攻击方式基本上在那里也能找到。
这篇文章假设使用一种叫做 AES 的加密算法,并使用 CBC 作为加密模式。
1. CBC 加密模式
CBC 的加密模式看起来时下面这个样子:
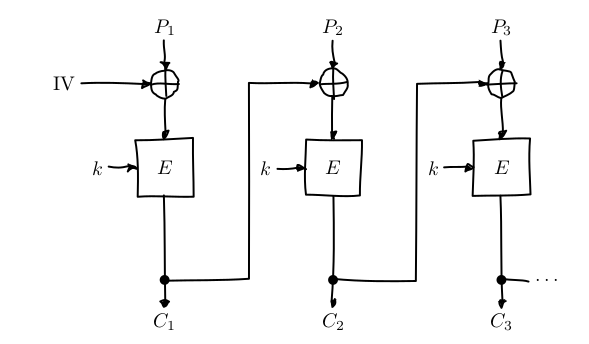
要加密 P, 先将分组,每组大小是固定的,这里分为三组 \( P=P_{1}P_{2}P_{3} \),第一组 \( P_{1} \) 首先和 IV 异或,后以 k 为密钥使用加密算法加密,生成第一组密文 \( C_{1} \), 生成的密文作为下一组加密使用的 IV,直到最后一组加密完成。
而 CBC 模式的解密与此类似:
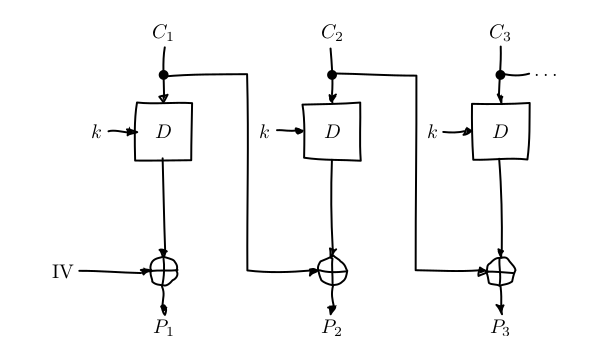
CBC 模式的参数有三个,\( P, k, IV \),C 是要加密的明文,k 是加密算法的密钥, IV 是 CBC 的初始向量。
2. 对可预测的 IV 的攻击
如果这个加密的 IV 是可预测的,那么攻击者可以猜测某个记录的一个字段 \( P_{i} \) 的值为 \( P_{x} \)。首先构造一个数据
\[ P_{M} = IV \oplus C_{i-1} \oplus P_{x} \]
发给服务端,服务端仍然将其加密:
\begin{align} C_{M} & = E(k, IV \oplus P_{M}) \\ & = E(k, C_{i-1} \oplus P_{x}) \\ \end{align}比较 CM 与 Ci 就知道猜测的明文是否正确。
3. 对使用 key 作为 IV 的攻击
假设使用 key 作为 IV, 密文为 \( C=C_{1}C_{2}C_{3} \),攻击者可以构造密文 \( C'=C_{1}ZC_{1} \) 给解密程序解密,其中 Z 值为 0。解开的明文为:
\begin{align} P'_{1}&= D(k, C_{1}) \oplus IV \\ &= P_{1} \\ \end{align} \begin{align} P'_{3} &= D(k, C_{1}) \oplus Z \\ &= D(k, C_{1}) \\ &= P_{1} \oplus IV \\ \end{align}攻击者获得 \( P'_{1} \) 和 \( P'_{3} \) 后, 可以计算
\begin{align} P'_{1} \oplus P'_{3} &= P_{1} \oplus P_{1} \oplus IV \\ &= IV \end{align}而 IV 就是 key。
4. CBC 位反转攻击
因为 CBC 使用上一个密文块与解密算法结果亦或得到明文,而密文块在传输过程中是可以被修改的,那么如果猜到 \( P_{i+1} \) 的值,就可以通过构造 X,令 \( C'_{i}=C_{i} \oplus X \) 来修改解密得到的 \( P_{i+1} \),从而产生预想的行为。比如将某个字段修改为 ";admin=1"。
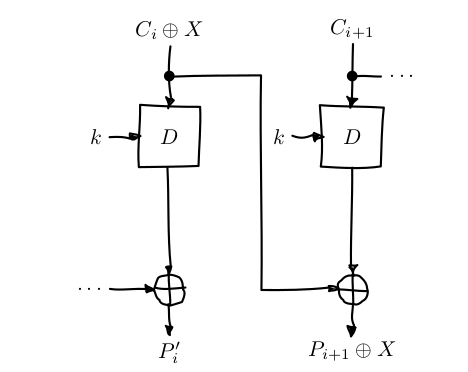
5. CBC 填充攻击
CBC 模式要求每个加密块都是固定大小的,如果不是固定大小,则将其填充到固定大小。如果使用 PKCS#5 或者 PKCS#7 算法填充,那么填充的值将是缺少的位数。
比如,如果每个块大小为 8 字节,那么填充的字节将是:
| 块长度 | 填充字节 |
|---|---|
| 0 | 08 08 08 08 08 08 08 08 |
| 1 | 07 07 07 07 07 07 07 |
| 2 | 06 06 06 06 06 06 |
| 3 | 05 05 05 05 05 |
| 4 | 04 04 04 04 |
| 5 | 03 03 03 |
| 6 | 02 02 |
| 7 | 01 |
如果接收端可以通知发送者解密是否失败,攻击者可以利用这个特征进行攻击。假设接收端如果发现填充的数字不符合长度要求,则不返回,而解密成功则有返回,返回内容为应用层数据出错或者返回执行成功。
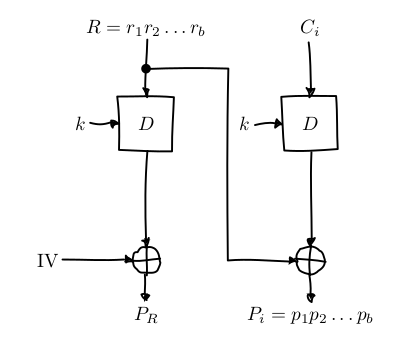
攻击者可以构造一个 R 作为密文,使得接收端解密后发现填充值是正确的。这很容易办到,只要枚举 R 的最后一个字节,直到接收端有返回为止。这是这里的主要攻击手段。
首先令 R=C, 然后依次尝试改变 R 的每个字节,直到没有返回。假设明文为
\[ p_0p_1p_2p_3p_4030303 \]
则依次改变字节,直到第一个 03 的位置,接收端没有返回: \[ p'_0p'_1p'_2p'_3p'_4050303 \]
这样就可以得到最后一个字节的值。下面假设最后一个字节为 01。那么
\[ D(C_i)[b] \oplus r_b = 01 \]
两边同时亦或 \( r_{b} \) 得
\[ D(C_i)[b] = 01 \oplus r_b \]
这样改变最后一个字节,使得 padding 增加一个字节:
\[ D(C_i)[b] \oplus r_b\oplus 01 \oplus 02 = 01 \oplus 01 \oplus 02 = 02 \]
随后枚举 \( r_{b-1} \) 直到有返回。此时
\[ D(C_i)[b-1] \oplus r_{b-1} = 02 \]
可以换算出
\[ D(C_i)[b-1] = 02 \oplus r_{b-1} \]
如此反复可以逐步获得明文。