传说中最安全的加密算法：一次一密

异或是一次一密的依赖的二进制二元运算符，运算符记为 \( \oplus \) 。如果运算符左右两边的比特位相同，则结果是0；如果运算符左右两边的比特位不同，则结果是1：

\begin{array}{ccc} 0\oplus 0 = 0 & 1\oplus 0 = 1 \\ 0\oplus 1 = 1 & 1\oplus 1 = 0 \end{array}

对于不是0和1的数值，可以按位异或，也就是将数值转为位二进制，然后按位异或。如：

\begin{aligned} 73 \oplus 87 & = 0b1001001 \oplus 0b1010111 \\ & = \begin{array}{*{7}{C{\widthof{$\oplus$}}}c} 1 & 0 & 0 & 1 & 0 & 0 & 1 & \quad \text{(left)}\\ \oplus & \oplus & \oplus & \oplus & \oplus & \oplus & \oplus & \\ 1 & 0 & 1 & 0 & 1 & 1 & 1 & \quad \text{(right)}\\ \end{array} \\ & = \begin{array}{*{7}{C{\widthof{$\oplus$}}}} 0 & 0 & 1 & 1 & 1 & 1 & 0 \end{array} \\ & = 0b0011110 \\ & = 30 \\ \end{aligned}

\(\oplus \) 有一些算数性质：

1. 顺序不影响最终结果： \(a\oplus \left(b\oplus c\right) = \left( a \oplus b \right) \oplus c \)
2. 交换律： \( a \oplus b = b \oplus a \)
3. 相同的数异或位0： \(a\oplus a = 0\)
4. 任何数与0异或，结果为原来的数：\(a\oplus 0 = a\)。
5. 异或某个数两次，结果不变： \(a\oplus b \oplus b = a\oplus \left(b\oplus b\right) = a\oplus 0 = a\)

根据上述性质5，就可以得出一次一密的原理：

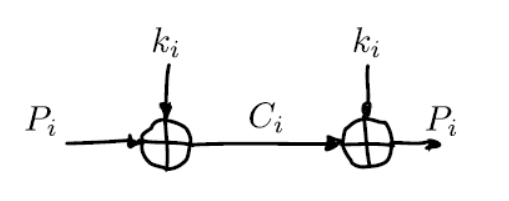
明文P异或密钥K得到密文C：\(P \oplus K=C\) 。密文 C 与密钥K异或还原为明文P: \(C\oplus K = P\) 。

攻击者拿到密文，不知道K的内容，就拿不到密文的信息（除了长度）。我们可以把 \(oplus\) 当作一个反转操作，对明文随机反转某些位获得密文，对密文按照明文的反转方式再反转以便还原明文。攻击者不知道密钥K，就不知道要反转哪些位。

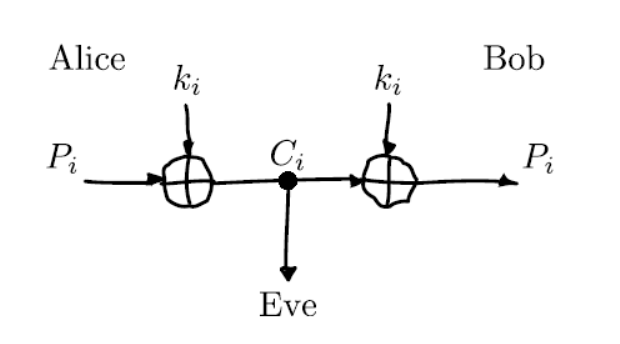
一次一密要点在于每个密钥只使用一次，而且完全随机不可猜测。密钥K通常使用真随机数生成器生成，写到磁盘后用飞机或货车运送，每次摘取其中一段 \( K[i..j] \)用于加密，一旦使用后，这一段 \(K[i..j]\) 就不能再使用了。

真随机数生成器并不神秘。举个例子：调整快门速度，用一束极光照射镜头，得出的照片每个像素点或明或暗，将明记为1，暗记为0，依次排列就是真随机数。

除了线下运送密钥，密钥还可以通过量子密钥交换算法(QKD)协商。

很明显，如果密钥K可以被猜测，攻击者很容易就能得出明文。例如，使用C语言的 rand() 函数，即时将时间戳传给 srand() ，攻击者多尝试几次就能获取所有随机数内容。

\(k\) 如果重复使用，攻击者截取两端密文 \(C_{1}\) 和 \(C_{2}\)，将其异或得到：

\begin{aligned} C_1 \oplus C_2 &= (P_1 \oplus K) \oplus (P_2 \oplus k) \\ &= P_1 \oplus K \oplus P_2 \oplus K \\ &= P_1 \oplus P_2 \oplus K \oplus K \\ &= P_1 \oplus P_2 \oplus 0 \\ &= P_1 \oplus P_2 \\ \end{aligned}

乍一看好像没啥用，因为必须要获得其中一段明文，才能计算得出另一断明文。但是，两端明文异或，仍然泄露了一些信息。比如我们使用相同的K加密两张图片：

循环使用密钥，还会出现另一个问题。当我们传输HTTP协议的数据时，有些明文内容是可以猜测的，如 "HTTP/1.1 200 OK"，以及 "Content-Type: " 等。猜测了这些位置的内容，异或就可以获得这些位置的K^'。那么下一轮再使用相同的密钥时，就可以使用这些已知的K^'还原对应位置的明文。反复猜测甚至能还原全部明文。