原地内存整理算法
Table of Contents
内存碎片化是内存回收器需要解决的问题之一。尽管堆中仍有可用空间,但是内存管理器却无法分配找到一块连续内存块来满足较大对象的分配需求,或者需要花费较长时间才能找到合适的空闲内存,这就是内存碎片化的问题。
要整理内存,以解决碎片问题,就要移动内存中的对象。对象移动后,原来指向对象的指针也要修改,指向对象新的内存位置。内存整理算法主要解决的问题就是保持指向对象的指针继续指向它这个约束,改变对象的位置以整理出大块空闲内存块。
1. 双指针算法
双指针算法(Two-Finger Algorithm)是整理算法中较为简单的一种。该算法通常假设所有内存对象的大小是固定的,或者至少是某种对齐粒度的倍数。
为什么需要整理固定大小的对象? 文中提到的疑问:“既然要求对象大小固定,还有什么整理的必要呢?”答案是:即使对象大小固定,使用空闲链表(Free List)进行分配虽然能找到空闲块,但会导致活跃对象在堆中分布零散(碎片化)。这会降低 CPU 缓存命中率(Locality)。通过整理,将所有存活对象移动到堆的一端,可以:
- 极大提高缓存局部性。
- 使后续的内存分配变得极其简单(只需移动一个指针,即 Bump Pointer Allocation),无需维护复杂的空闲链表。
**算法特点**:
- **任意顺序(Arbitrary Order)**:整理后对象的顺序与原顺序无关。
- **两次遍历**:第一次移动对象,第二次更新指针。
- **限制**:通常仅适用于固定大小对象,且不保持对象原有顺序。
(1.1) 第一次遍历初始化时,指针 free 指向区域初始位置(堆头),scan 指向区域末端(堆尾)。
(1.2) 随后不断向前移动指针 free, 直到遇到一个空闲位置 (没有"-"的位置);同时不断向后移动指针 scan,直到遇到一个存活对象。
(1.3) 如果 free 和 scan 发生交错(free > scan),第一次遍历结束。
(1.4) 将 scan 指向的对象移动到 free 的位置。 **关键点**:scan 指向的原位置(现在是空闲的)必须记录下对象移动到了哪里(即 free 的地址)。通常会在原位置写入一个转发地址(Forwarding Address)。随后将 scan 处的内存标记为空闲(或逻辑上视为已处理)。随后跳转执行 (1.2)。
(2.1) 第二次遍历初始化时,scan 指向区域初始位置(或者是根集合 Roots)。
(2.2) 遍历所有根指针和堆中已移动对象的指针域。
(2.3) 如果某个指针指向的地址 > scan (即指向了旧的堆尾区域),则读取该旧地址处的转发地址,更新指针指向新的位置。
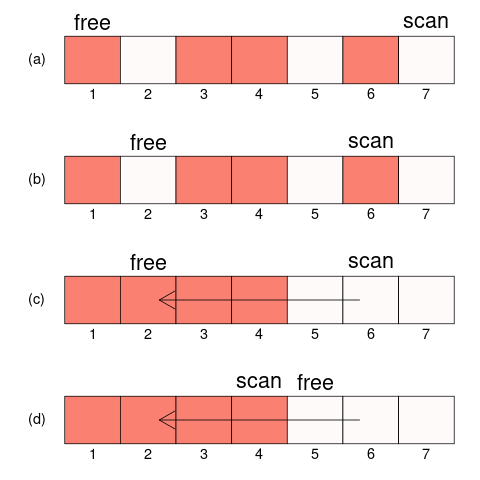
Figure 1: 双指针算法示意图
用上图的流程举例,(a) 初始化; (b) free 找到第一个空闲位置, scan 找到第一个存活对象; (c) 将 scan 指向的对象转移到 free 指向的空闲位置; (d) free 和 scan 继续前几, 两者交叉,第一次扫描结束。第二次扫描将所有指向 6 的指针改为指向 2。
2. Lisp 2 整理算法
Lisp 2 回收算法可以说是历史悠久,同时也得到了广泛应用。尽管需要三次遍历,但每次遍历要做的工作都不多。虽然标记-整理回收算法的吞吐量都比较低,但一些研究发现 Lisp 2 在整理式回收算法中算是最快的。它的缺陷在于,需要每个对象头部都额外增加一个完整的域(forwardingAddress)来记录转发地址。
Lisp 2 需要三次遍历。
(1) 第一次遍历将所有存活对象的 forwardingAddress 域指向最后要移动到的地址。
(2) 第二次遍历将所有指向存活对象的引用都修改为相应对象的 forwardingAddress。
(3) 第三次遍历将所有存活对象转移到 forwardingAddress 中。
compact(): computeLocations(HeapStart, HeapEnd, HeapStart) updateReferences(HeapStart, HeapEnd) relocate(HeapStart, HeapEnd) computeLocations(start, end, to) scan <- start free <- to while scan < end if isMarked(scan) /* marked 过的对象是存活的 */ forwardingAddress(scan) <- free scan <- scan + size(scan) updateReferences(start, end): for each fld in Roots ref <- *fld if ref != null *fld <- forwardingAddress(ref) scan <- start while scan < end if isMarked(scan) for each fld in Pointers(scan) if *fld != null *fld <- forwardingAddress(*fld) scan <- scan + size(scan) relocate(start, end): scan <- start while scan < end if isMarked(scan) dest <- forwardingAddress(scan) move(scan, dest) unsetMarked(dest) scan <- scan + size(scan)
3. 引线整理算法 (Threading / Pointer Reversal)
引线整理算法(Threading Compaction),也称为指针反转(Pointer Reversal)算法。它通过一种巧妙的策略解决指针更新的问题,并且**不需要额外的域**来保存转发地址(相比 Lisp 2 节省了空间)。
**核心思想**:利用对象中原有的指针域来临时存储链表信息。一次“引线”操作是将指向某对象的所有指针连接成一个链表,链表的头保存在该对象中。当转移这个对象时,可以通过这个链表找到所有指向它的指针,并更新它们。
**缺点**:由于算法在运行过程中会临时修改(破坏)对象中的指针域,所以**并不适合并发回收器**,因为在整理过程中对象处于不一致的状态。
引线过程如下图所示:
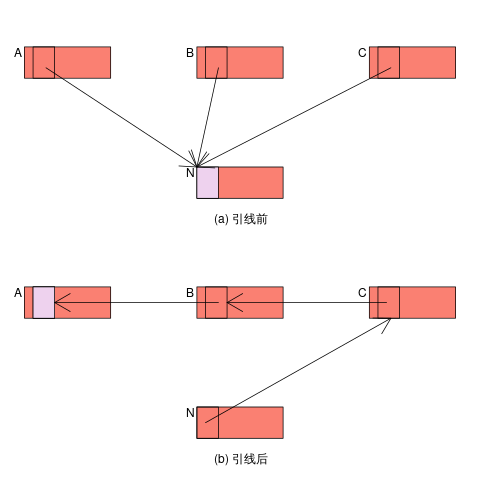
Figure 2: 引线示意图
引线前,A, B, C 都有一个指针域指向 N, 引线后, N 中的一个域作为链表的头指向 C 中指向 N 的指针, C 中指向 N 的指针指向 B 中指向 N 的指针, B 中指向 N 的指针指向 A 中指向 N 的指针。因为 A 是链表的尾部,所以 A 中原来存放指针的位置可以保存 N 处已经指向 C 的指针的位置的信息。
引线整理算法需要两次遍历,第一次实现引线,以及前向指针的逆引线;第二次实现后向指针的逆引线。
compact(): updateForwardReferences() updateBackwordReferences() thread(ref): // 引线,即反转一个指针 ... update(ref, addr): // 逆引线, ref 为链表头的下一个位置,addr 为链表头 ... updateForwardreferences(): for each fld in Roots thread(*fld) free <- HeapStart scan <- HeapStart while scan <= HeapEnd if isMarked(scan) update(scan, free) // 将所有指向 scan 的前向指针改为 free for each fld in Pointers(scan) thread(fld) free <- free + size(scan) scan <- scan + size(scan) updateBackwordreferences(): free <- HeapStart scan <- HeapStart while scan <= HeapEnd if isMarked(scan) update(scan, free) // 将所有指向 scan 的后向指针改为 free move(scan, free) free <- free + size(scan) scan <- scan + size(scan)
4. 单次遍历算法
单次遍历算法用一个位图标记存活的内存对象,并将内存分成大小相等的块,每个块第一个存活对象的转发地址将记录在偏移向量中,块中其它对象的偏移地址通过块大小和块中存活对象的数量与大小实时计算。
compact(): computeLocations(HeapStart, HeapEnd, HeapStart) updateReferencesRelocate(HeapStart, HeapEnd) // 计算每个内存块第一个存活对象的偏移地址 computeLocations(start, end, toRegion): loc <- toRegion block <- getBlockNum(start) for b <- 0 to numBits(start, end) - 1 if b % BITS_IN_BLOCK = 0 offset[block] <- loc // 块中第一个对象的偏移地址 block <- block + 1 if bitmap[b] == MARKED loc <- loc + BYTES_PER_BIT // 根据存活对象大小增加 // 计算对象的偏移地址 newAddress(old): block <- getBlockNum(old) return offset[block] + offsetInBlock(old) // offsetInBlock 通过位图计算 updateReferencesRelocate(start, end): for each fld in Roots ref <- *fld if ref != null *fld <- newAddress(ref) scan <- start while scan < end scan <- nextMarkedObject(scan) for each fld in Pointers(scan) ref <- *fld if ref != null *fld <- newAddress(ref) move(scan, newAddress(scan))
5. 总结与对比
| 算法 | 遍历次数 | 空间开销 | 对象顺序 | 适用场景 |
| :--- | :—: | :—: | :—: | :--- |
| 双指针 (Two-Finger) | 2 | 无 | 任意 (乱序) | 固定大小对象,对局部性要求不高 |
| Lisp 2 | 3 | 高 (Header) | 保持原序 | 通用,实现简单,吞吐量尚可 |
| 引线 (Threading) | 2 | 无 | 保持原序 | 内存受限环境,不适合并发 |
| 单次遍历 (One-Pass) | 1 | 中 (Bitmap/Table) | 保持原序 | 实时性要求高,需要额外辅助结构 |
- **双指针**最快但打乱了顺序,且局限于固定大小。
- Lisp 2 是最经典的滑动整理(Sliding Compaction),保持了分配顺序(即保持了局部性),但需要额外的头部空间。
- **引线算法**用时间换空间,不需要额外空间但操作复杂。