Amdahl 定律
Table of Contents
并行,是目前计算机领域性能优化的主要方法。指令级并行让编译器优化技术火热好几年,近年数据级并行因为人工智能的普及也有不小的发展。分布式架构、微服务、云原生,让软件的并行变得更简单。
在实际软件工作中,经常被人问道类似的问题:你3个服务器可以支持10万设备的业务,那客户那边有3000万设备,用900个服务器是不是就可以满足要求?并不是这样算的。并行和横向扩展 (scale out) 受到 Amdahl 定律的约束,不能随节点数量的增加线性增长(Linear)。(实际上按照我们当时的软件结构,再加多少服务器也达不到那个客户的业务要求(小声唧唧歪歪。
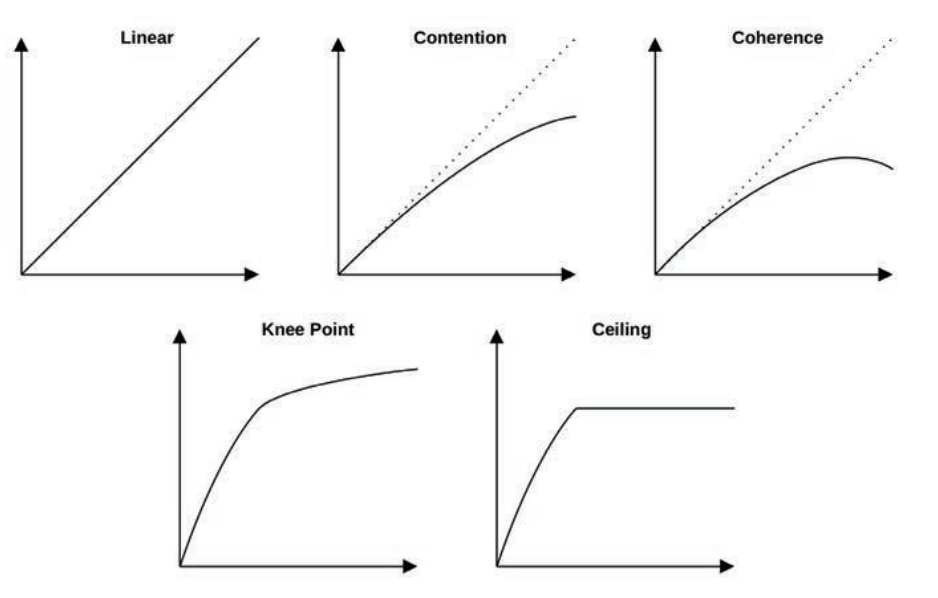
Ambdahl's law (安姆达定律,或安达尔定律),是性能优化、横向扩展的理论依据之一。
1. Amdahl 定律公式
Amdahl 定于描述性能优化的极限。我们定义性能优化程度 S (Speedup) 为优化后性能与优化前性能的比值:
\[ S = \frac{Performance\ using\ the\ enhancement}{Performance\ not\ using\ the\ enhancemanet} \]
也可以是优化前执行时间除以优化后的执行时间:
\[ S = \frac{Execution\ Time\ without\ using\ the\ enhancement}{Execution\ Time\ using\ the\ enhancemanet} \]
比如说,我们有一个 Python 编写的 quick and dirty 固件扫描器,扫描一个固件需要1小时;重新设计算法、使用并行任务、并使用 C 语言重写后,扫描一个固件需要 20 秒。我们说这次性能优化了 180 倍 (S=180)。
换句话说,我们有一个 Python 编写的 quick and dirty 固件扫描器,扫描速度是每小时1个固件;重新设计后,扫描速度是每小时180个固件。我们说这次性能优化了 180 倍。
有人问真的优化真么多吗?到少算高是根据实际系统来定的。我遇到的案例中,10倍以下的优化是不值得做的。我们公司常有人喜欢找一个小功能优化了20%~30%,算上他人工成本和让其他员工理解他的设计而用来培训的时间,以及增加的开发难度来看,不光钱花的更多,还容易错过市场窗口期。上面说的固件扫描器的例子,在没有卖出超过 2000 份之前,我们是不愿意为了这 180 倍的性能提升去重新写一份代码的。
Amdahl 定律把一个系统分为两个部分:可优化的部分 \(p\) ,和不可优化的部分 \(1-p\) 。(这里 "可优化" 意思是使用这个技术可以提升性能的那部分;" 不可优化" 意思是这次优化使用的技术不能让这部分有性能提升。)
例如,上面的例子中,我们修改了代码,同一个任务的指令数量变少了,但是整个固件还是要读取出来。软件程序从磁盘读取文件到内存这个IO过程使用了1秒,使用代码匹配特征这个过程用了 59 分 59 秒。这次修改中,IO 过程是不可优化的,特征匹配的过程是可优化的。可优化的部分里面,从 59 分 59 秒优化到 19 秒,可优化部分性能提升 \( s = 179.75 \) 倍。
在使用一个优化后,整个系统的执行时间是:
\[ E_{new} = E_{old} \times \left( (1-p) + \frac{p}{s} \right) \]
\( E_{new} \) 是优化后执行一个任务的时长;\( E_{old} \) 是优化前一个任务消耗的时间;\( p \) 是可优化的部分在整个系统中的百分比; \( s \) 是可被优化的部分这次性能提升多少。
整个系统的优化的倍数为:
\[ S_{overall} = \frac{E_{old}}{E_{new}} = \frac{1}{(1-p)+\frac{p}{s}} \]
从公式可以看出,最差的情况是可优化部分是0,不管证明扩展优化,都没有好处。最好的情况是系统 100% 可以优化,优化倍数就是 \(s\)。其它情况,可优化部分大于0小于1,想要优化的越多,优化的性价比 (\(S_{overall}\) 与 \(s\) 的比值)就会越低。
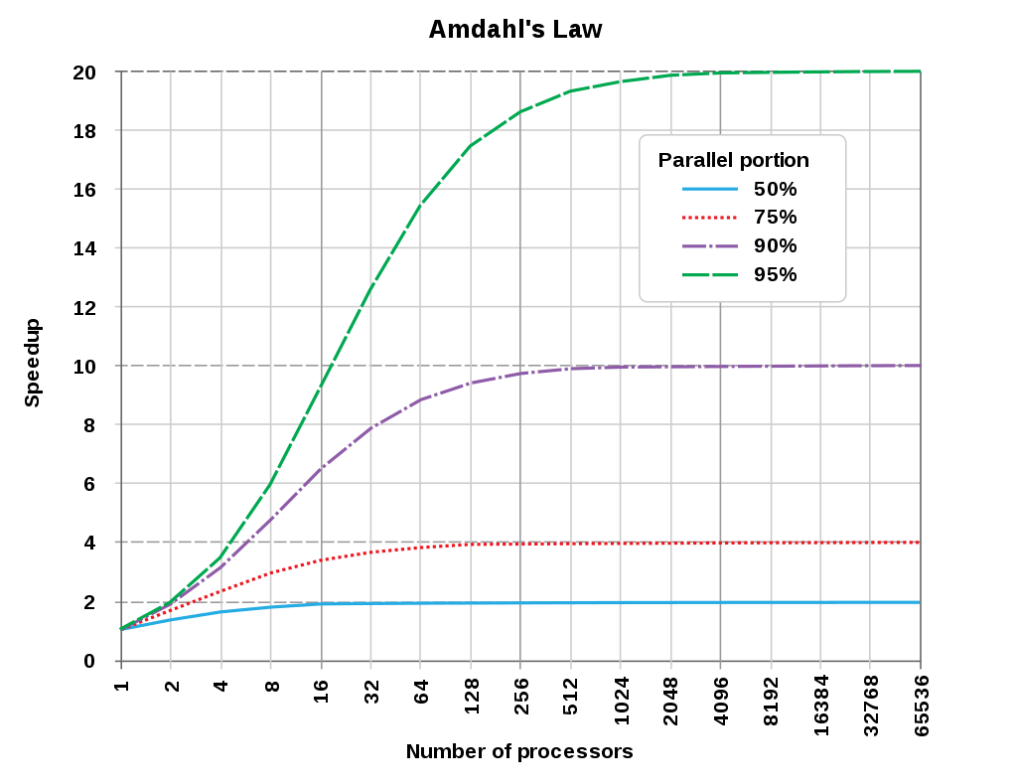
2. 实际应用
(1) 实例1:给服务器换CPU
假设我们要给一个网站的服务器换一块 CPU,新 CPU 性能是老 CPU 的 10 倍。原来老服务器上分析,程序 40% 的时间在运行计算任务,60% 的时间在等待 IO。如果 CPU 换上,整体性能可以提升多少?
\[ S_{overall} = \frac{1}{(1-p)+\frac{p}{s}}= \frac{1}{0.6+\frac{0.4}{10}}\approx 1.56 \]
现在我们知道给这个服务器买新的 CPU 有多亏了。
(2) 实例2:选优化方案
我们有一个商用程序,实际应用中,调度库占总执行时间的一半,其中的几何规划功能占总执行时间的 20%。我们有两个优化方案:a 是优化几何规划算法,使其执行速度提升 10 倍;b 是优化底层数学库,使得调度库执行速度整体提升 1.6 倍。使用哪个方案更好?
\[ S_{a} = \frac{1}{(1-0.2)+\frac{0.2}{10}} = 1.22 \]
\[ S_{b} = \frac{1}{(1-0.5)+\frac{0.5}{1.6}} = 1.23 \]
看起来差不多,b 方案好一轻微点点。
(3) 实例3:多线程
在一个 4 核系统上,一个单线程的程序,20% 的部分是不能并行的,80% 的任务可以并行。我们使用多线程方案优化它的执行时间,理论上最多可以优化多少?
\[ S_{3} = \frac{1}{(1-0.8)+\frac{0.8}{4}}=2.5 \]
(4) 实例4:重构
我们把实例3的代码重构了,使得 90% 的部分可以并行。那么最多可以优化多少?
\[ S_{4} = \frac{1}{(1-0.9)+\frac{0.9}{4}} \approx 3.08 \]
(5) 实例4: 换多核 CPU
实例3运行在4核心的系统上,使用实例3的多线程方案,换成6核心,可以优化多少?
\[ S_{5} = \frac{1}{(1-0.9)+\frac{0.9}{6}} = 3 \]
3. Amdahl 公式其他形式
有些地方使用一个看起来更容易计算的公式。令 \(f=1-p\) 为不可优化的部分所占比例,那么。
\[ S=\frac{1}{(1-p)\frac{p}{s}}=\frac{s}{s(1-p)+p}=\frac{s}{1+(s-1)f} \]
其中小写 \(s\) 是可优化的部分提升比例。在横向扩展中,可以是服务器数量。
这个公式在《Systems Performance: Enterprise and the Cloud》 一书中写成这样:
\[ C(N) = \frac{N}{1+\alpha(N-1)} \]
4. Amdahl 定律的局限
Amdahl 定律是个理论值,在横向扩展问题里,它假设加一个服务器,执行某个部分的任务的速度就会增加多少倍,忽略了沟通的成本。服务器越多,网络通信也将会也多,增加的协调成本也会更高。这部分消耗被 Amdahl 定律忽略了。
考虑横向扩展的时候,有人会更喜欢使用 Universal Scalability Law:
\[ C(N) = \frac{N}{1+\alpha (N-1)+\beta N (N-1)} \]